Mental health and natural land cover: a global analysis based on random forest with geographical consideration

Data information

Survey information

Our study employs an international survey conducted by Kyushu University, Japan, from July 2015 to March 2017, covering 37 countries, including both developed and developing countries. Gallup executed the survey in each country through online and/or face-to-face methods. Gallup is the most experienced team in the global well-being survey, so the survey was able to represent each country’s demographics based on their sampling database. The investigation periods for each country were generally less than one month. The survey team created a matrix representing different age groups and genders to align with the demographics of the general population. Subsequently, they conducted recruitment and gathered responses until each cell in the matrix was filled. Moreover, to guarantee the reliability of the survey, the same questionnaires were used, while currency-related questions were based on local currencies. The population and GDP of these countries accounted for 68.58% of the global population and 82.67% of the worldwide GDP in 2017, respectively (Supplementary Material Table S2). This survey obtained self-reported individual mental health and several other demographic and socioeconomic characteristics. The total number of observations that were recorded was 100,956. However, due to a lack of geographical location or records, 95,571 observations were kept. In addition, because some individuals did not provide income information, 89,273 observations are used in the current calculations (descriptive statistics of the features shown in Supplementary Material Table S3). Except for geographical location and income information, for each respondent, all other variables of interest are completely and validly fulfilled.

The ethics review committee for Kyushu University, Japan approved all experimental protocols used for the survey, and all methods were carried out according to the relevant guidelines and regulations. All survey methods were carried out following relevant guidelines and regulations. At the beginning of the survey, respondents were informed about the survey’s aim and their rights to participate voluntarily. All respondents provided informed consent before responding to the questionnaire.

Mental health

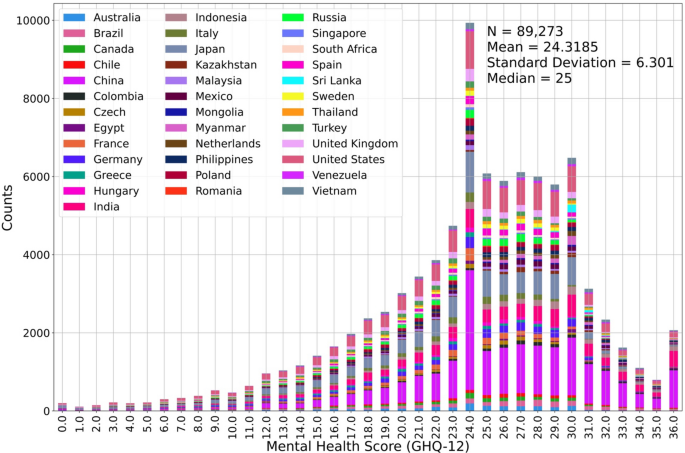
We include the twelve-item General Health Questionnaire (GHQ-12) in the survey to assess individual mental health. The GHQ-12 is a widely used self-report tool designed to evaluate an individual’s mental health and psychological well-being, commonly employed in clinical and research contexts^42,43,44. The GHQ-12 comprises 12 items that aim to assess an individual’s experience over a specified period using a Likert scale. These 12 items ask the respondents to answer whether they have recently “(1) been able to concentrate on whatever you are doing?”, “(2) lost much sleep over worry?”, “(3) felt that you are playing a useful part in things?”, “(4) felt capable of making decisions about things?”, “(5) felt constantly under strain?”, “(6) felt you could not overcome your difficulties?”, “(7) been able to enjoy your normal day-to-day activities?”, “(8) been able to face up to your problems?”, “(9) been feeling unhappy and depressed?”, “(10) been losing confidence in yourself?”, “(11) been thinking of yourself as a worthless person?”, and “(12) been feeling reasonably happy, all things considered?”. Each item of the GHQ-12 has four potential answer options, specifically, “not at all,” “no more than usual,” “rather more than usual,” and “much more than usual,” arranged from the most negative value represented by 0 to the most positive value represented by 3. For example, for the question (1), if the participant’s answer is “much more than usual,” the score of this question should be 3, because this question is positive direction, whereas for the question (2), the same answer would rate as 0, since this question is negative direction. The mental health assessment score is computed as the summed score of all 12 items. Thus, the output variable of our study is a discrete numeric variable ranging from 0 to positive. The current random forest method is designed to execute either regression or classification. The algorithm performs the classification task using the discrete output variable, assuming the output is categorical. However, adjacent scores of the mental health assessments are related; i.e., they are ordinal rather than categorical. Figure 1 illustrates the statistical distribution of the mental health assessment scores. Most people receive 24 points in the assessment, and significantly more people score between 24 and 30 points than other range. In this situation, if we were to perform the random forest classification, then the classification accuracy for the people with lower or higher scores would be extremely low due to the unbalanced output distribution. Thus, we assume that the mental health assessment score is continuous.

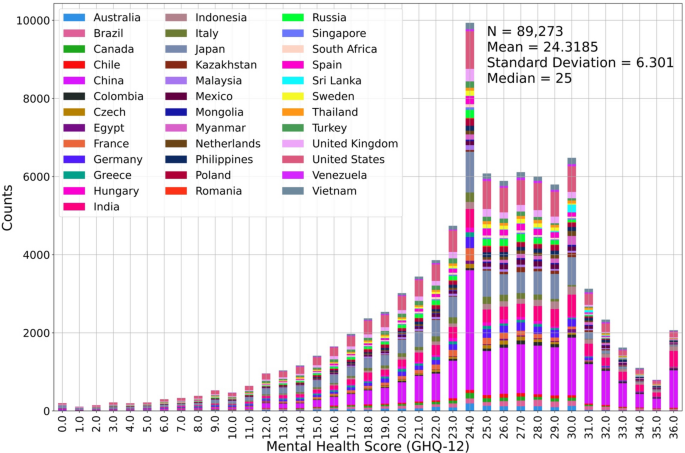
The statistical distribution of mental health assessment (the color blocks are arranged alphabetically from bottom to top according to the first letter of the country. Detailed numbers are listed in Supplementary Materials Table S1).

Global land cover data

For the land cover, we use remote sensing data compiled by Tsinghua University, China (http://data.ess.tsinghua.edu.cn/), because, to our knowledge, it is the dataset with the highest global resolution, at approximately 30 m. This dataset provides information on the 2017 global land cover. It classifies land cover into ten categories: cropland, forest, grassland, shrubland, wetland, water, tundra, urban land, bare land, and snow/ice³⁵. We calculate the areas of each land type surrounding our survey respondents with these data. To estimate the impact of land cover in our analysis, we use the percentages of each land type within a radius of 5000 m around each respondent,following a previous study³⁰. Previous theory indicates that distance and accessibility to the natural environment would influence the relationship between land cover and mental health⁴⁵. However, in large spatial analyses, especially multi-regional studies^29,30,31, using a land cover ratio within a certain distance is still acceptable, because with a higher ratio of a land type, the residents have a higher possibility to access that land type or do some activities in that land type. Eight land types are used to examine the land cover data; the tundra and snow/ice land types are rarely present within the analyzed area. After running the random forest analysis, we estimate the Shapley values of each land type. In this study, we regard urban land as artificial land cover, while other types are considered natural.

Other control variables

We add several other control variables because mental health status may differ according to people’s socioeconomic and demographic characteristics; these variables are age, gender, employment, educational background, the ratio between individual income and GDP per capita in the respondent’s country (RI) (RI’s computation is summarized in Supplementary Materials), emotion in the surveyed week, number of children, self-reported health, self-reported personality, and evaluation of living environment. Among these control variables, employment, educational background, and self-reported personality are categorical. We use the one-hot encoding method to convert them into a series of dummy variables. Thus, every respondent has 49 features and one output variable in the analysis. Importantly, we include emotions in the past week to illustrate the emotional well-being; these emotions are “pleasure”, “anger”, “sadness”, “enjoyment”, and “smile”. Emotional well-being is a factor of mental health⁴⁶. The GHQ12 is considered an aggregated score of mental health. Although there are some similar aspects between emotional well-being and the GHQ-12, we investigate each emotion’s impact on mental health by employing it as an independent variable. The descriptions of the features are listed in Supplementary Materials Table S4.

Data analysis

Model pre-selection

To detect influential factors on mental health and confirm the relationship between mental health and land cover, linear regression methods, such as OLS and ordered logistic regression (OLR), are widely applied, e.g., Ref.^6,28,38,47. These studies evaluate the monetary values of land cover through OLS estimation because OLS is straightforward to explain. Additionally, the investigations that employ the OLR are theoretically more reasonable since mental health evaluation is used as a discrete variable rather than a quantitative and continuous variable in most studies^6,38. OLR is a typical classification function based on logistic regression. However, these two models rely on linear assumptions and thus cannot directly illustrate the importance of predictors on the outcome variable. Stated another way, based on the linear assumption, a 1-unit increase in a certain land type always has the same effect on an individual’s mental health, whatever is the status quo. This is not consistent with the actual situation. Generally, when the computational complexity of the algorithm matches the complexity of the data, the fitting results are better. Linear models’ computational complexity is relatively lower, so they cannot fit the relationships with high accuracy, in a word, under-fitting. Machine learning methods with higher computational complexities, including support vector machine (SVM), tree-based boosting models, and multi-layer perceptron (MLP), are able to grasp the non-linear relationship, which is closer to real-world situations.

In the pre-selection stage, we compare several potential models, which are OLS, OLR, SVM, adaptive boosting (AdaBoost), gradient boosting model (GBM), extreme gradient boosting (XGBoost), random forest, and multi-layer perceptron (MLP). To select the highest performance model, we test all models, except MLP, with the defaulted parameters based on tenfold cross-validation. It must be noted that we built an MLP with a similar computational complexity as XGBoost, because XGBoost has the largest computational complexity. We use the widely used equation toughly estimate the computational complexity of XGBoost. Then, based on the estimation number, an MLP’s hyperparameters, including the number of hidden layers, the number of nodes in the hidden layers, and the number of training epochs, are selected. Of course, more detailed fine-tuning, feature engineering, and hyperparameter adjustment might improve the performance of the MLP. Limited by the current computing power, we are unable to do more tests. However, to some degree, the current MLP still could be a reference to be compared with other basic models. The MLP has 22 layers, wherein one input layer, 20 fully connected layers, and one output layer. The input layer has 49 input nodes. Each fully connected layer has 100 nodes. The output layer has one output node. In total, this MLP has 207,101 parameters to train. The activation function of the fully connected layers and the output layer is “ReLU”. The MLP’s adaptor is “Adam”, the batch size is 32, and we train the MLP 20 epochs. The tenfold cross-validation average accuracies of OLS, OLR, SVM, AdaBoost, GBM, random forest, XGBoost, and MLP are 42.55%, 13.43%, 33.40%, 22.62%, 46.01% 47.34%, 47.19.%, and 44.67%, respectively, as shown in Table 1. Since our task is regression, we are also interested in root mean square error (RMSE), mean square error (MSE), and mean absolute error (MAE). Among eight potential models, OLR is for classification tasks, so RMSE, MSE, and MAE are not suitable for this method. It should be explained that RMSE and MSE are sensitive to outliers. RMSE is the same as the target variable, while MSE is more impactful. MAE is another robust measure of error when there are extreme values in the analysis. The RMSEs of OLS, SVM, AdaBoost, GBM, random forest, XGBoost, and MLP are 4.77, 5.14, 5.54, 4.63, 4.57, 4.58, and 4.65, respectively. The MSEs are 22.80, 26.44, 30.71, 21.43, 20.90, 20.96, and 21.61, respectively, and the MAEs are 3.65, 3.81, 4.52, 3.51, 3.42, 3.47, and 3.55, respectively. In terms of four indices for regression, namely R², RMSE, MSE, and MAE, the random forest’s performance is the best.

In terms of the survey data, the random forest is a suitable model. The basic element, decision tree, of the random forest method has no assumption about data distribution, different from OLS and OLR. In fact, some features used in our analysis are mainly binary variables such as gender, job, and educational background, while others are discrete, such as age and RI. A decision tree is based on numerous binary judgments, so it is extremely suitable for analyzing our data.

Random forest

The random forest method builds a barrage of decision trees in parallel and allows them to vote for the results⁴⁸. The voting strategy for regression takes the average value of all individual predictions as the random forest prediction. Bagging and bootstrapping are performed to guarantee the accuracy and reliability of random forest⁴⁹. Bootstrapping is the sampling technique used by random forest. First, we set the number of trees in our random forest as \({N}_{tree}\). We extract \({N}_{tree}\) samples with replacement from the original data, and the sample sizes are 2/3 of the data of the total sample. Every decision tree utilizes the bootstrapped dataset. However, at most, a predefined number of random features (\({N}_{features}\)) are used in a single decision tree rather than all the features. After training, the random forest model can predict the output variable by aggregating the votes from each tree. Using the bootstrapped dataset and the aggregate of votes, this process is terminologically called “bagging”. Additionally, approximately 1/3 of the total sample is left out from the training process, which is called the out-of-bag (OOB) dataset. The OOB dataset is applied to test the accuracy of the random forest model through the OOB score, which is the proportion of OOB observations correctly predicted by the trained random forest. The reliable trained models have a relatively high OOB score.

In random forest, most parts are built randomly, while only three critical parameters must be decided by the users, specifically, the minimum number of remaining observations in end leaves (\({N}_{remain}\)), \({N}_{tree}\) and \({N}_{features}\). First, the minimum number of observations in the end leaves decides where the split stops because our random forest follows the greedy approach. If \({N}_{remain}\) is too small, the decision tree might be too deep and too many end leaves would be generated, which could cause the model to be large and even unavailable to the computer memory. Moreover, the random forest accuracy will increase to some extent when more trees are included. However, the cost of infinitely increasing \({N}_{tree}\) is a dramatic increment of calculation power and calculating time. Additionally, when \({N}_{tree}\) exceeds a particular value, the marginal effect of increasing the number is minimal. Accordingly, considering the size of our dataset and computing ability, the number of trees is set to 1,000. Moreover, the number of features used in the decision trees, \({N}_{features}\), is another vital factor. A large \({N}_{features}\) might reduce the model’s ability to grasp the relationship, while a small \({N}_{features}\) might cause underfitting. Previous studies have indicated that roughly one third of the total number is recommended^48,49,50. Thanks to our relatively sufficient computing ability of a high-performance computer, we test the most possible \({N}_{features}\) values based on tenfold cross-validation. According to the test, the goodness of fit peaks when the \({N}_{features}\) value is 11 (the hyperparameter process is summarized in Supplementary Materials Table S5). We also test several possible \({N}_{remain}\) values, including 2, 5, 10, 15, 20, 25, 30, 35, and 40, based on tenfold cross-validation. Although the results show that with the same \({N}_{features}\) and \({N}_{tree}\), a smaller \({N}_{remain}\) causes a higher cross-validation score, the improvement is limited. For example, the increase in \({N}_{remain}\) in the cross-validation score from 2 to 10 is not more than 1%. However, the disadvantage of the smaller \({N}_{remain}\) is obvious. When we build the connection between the Shapley value and the values of features locally, the limited local datasets might make the connection coefficient nonsignificant. Due to the trade-off, we set \({N}_{remain}\) as 30. In plain language, each decision tree randomly picks 11 features from the dataset, and each end leaf includes at least 30 observations.

In this study, we employ the geographical coordinates of each respondent in the fitting process. In other words, our random forest model is apt to assign geographically close respondents to the same branch. This way is more effective than employing country variable. The division of the model is the basis of geographically local dataset. The latter stages, namely random forest model explanation and the connections between observed and explanation values, are based on the locally geographical environments. In this way, we do not need to use administrative regions to reduce mental health variations among countries and regions. This method should be more valid and reasonable. Changes in mental health are geographically continuous rather than abrupt. To clarify the difference between continuous variation used in our research and abrupt change employing country variables, we provide a simple example here. Assume that there are two respondents who are completely the same living close to the national boundary, such that respondent A and B belong to two different countries, i.e., countries A and B, respectively. Although there could not be large difference between the living environments of respondents A and B, the model predictions for those two respondents might be dramatically different. In contrast, our method divides the large dataset into numerous local datasets based on geographical information. Every respondent could be included in several local datasets. Geographically, the variation in local datasets is continuous. We investigate the local connections within each local dataset. Therefore, these local connections are also geographically continuous and spatially varied, and it is not necessary to employ the country variable.

Variable importance

Random forest could estimate the importance of each feature on the output variable. The basic idea of importance estimation in random forest is to calculate the reduction in accuracy before and after excluding a specific feature⁴⁸. The reduction in the accuracy of a particular feature would be higher when it is more important to successfully predict the output variable compared with other features. This reduction is similar to the partial R² in the OLS algorithm. There is no need to select the features in the random forest algorithm since issues, such as multicollinearity, do not influence the accuracy of the random forest algorithm. However, multicollinearity is a fatal problem in OLS.

Shapley additive explanations (SHAP)

Although the accuracy of random forest is high, it is challenging to understand and explain the results^41,51,52. Shapley additive explanations (SHAP) is an advanced approach that aims to explain the contributions of each feature locally based on theoretically optimal Shapley values⁴⁰. To explain the contributions of features, each feature of the observation is a “player” in a game, and the prediction value is the payout. Shapley values help us fairly distribute the payout among the players^40,53. The Shapley value of a feature value is estimated as follows:

where \(x\) represents a specific observation of interest, \(j\) represents a particular feature of interest, \({S}_{jx}\) represents the Shapley value of the feature \(j\) of the observation \(x\), \(J\) represents a permutation of the set of indices \(\left\{1, 2,\dots ,p\right\}\) corresponding to an ordering of \(p\) features included in our random forest model, \(\pi (J,j)\) represents the set of the indices of the features contained in \(J\) before the \(j\)-th variable, and \({g}^{j|\pi (J,j)}(x)\) represents the estimated contribution value of feature \(j\) of the observation \(x\) with a specific permutation. \({g}^{j|\pi (J,j)}(x)\) is calculated as follows:

where \(X\) represents a matrix of random values of features, \(f()\) represents our trained random forest model, \(E\left(f\left(X\right)|{X}^{1}={x}^{1},\dots ,{X}^{j-1}={x}^{j-1},{X}^{j}={x}^{j}\right)\) is the expected value of the predictions of \(X\), when we set \({X}^{1}={x}^{1},\dots ,{X}^{j-1}={x}^{j-1},{X}^{j}={x}^{j}\), and \(E\left(f\left(X\right)|{X}^{1}={x}^{1},\dots ,{X}^{j-1}={x}^{j-1}\right)\) is the expected value of the predictions of \(X\), when we set \({X}^{1}={x}^{1},\dots ,{X}^{j-1}={x}^{j-1}\). \(X\) is used to complish the predictions based on the trained random forest model, \(f()\). Importantly, generally, the random values are deemed to have no explanatory ability. However, the random feature values in \(X\) must belong to a range of feature values and have the same numerical characteristics. Each row in \(X\) could be regarded as a real individual. Therefore, in real computations, the random dataset \(X\) is not randomly generated but instead randomly picked up from our dataset. In the SHAP estimation, some features would be replaced by the aimed individual’s certain feature value. Of course, if features, even a feature, are different between two rows, we could regard them as two different individuals. When a part of \(X\) is replaced, it does not represent the real individuals from our survey anymore. In our analysis, we set the dataset size of \(X\) as 1000, approximately 1% of the total dataset, according to the python package makers’ recommendation⁴¹. We must emphasize that all features’ contributions to mental health for each observation, \(x\), are estimated. \(X\) is simply a random matrix; it does not represent the total dataset^41,53. A larger dataset size here would definitely increase the computation time. To estimate the Shapley values efficiently, we use 4048 random permutations of all features. Of course, more permutations lead the estimated values to the real values, but the computing time is not affordable.

The connection between features’ values and their SHAP values

The explanations of SHAP values are too local. One observation’s SHAP values illustrate only one individual’s particular situation and thus cannot be directly used on other observations. A SHAP value is the feature value’s contribution to each observation’s current mental health status. For example, in one observation’s living environment, urban land comprises 99.60% of the total, and its SHAP value is -0.009. This individual’s living environment is monotonous and full of urban land, which might negatively affect her or his mental health. For another observation, urban land comprises 73.98% of the total, and its SHAP value is 0.012. The impacts of a certain feature on an individual’s mental health might be associated with his or her the current status. We employ linear regression to probe the relationship between a feature value and its contribution to mental health. However, since this research is global, a huge spatial extent makes the globally unified relationship suspicious. Estimating the relationship locally is more rational. Based on the local regression, although the relationships are locally linear, they are globally nonlinear.

Building a series of local datasets is the critical aspect. In the model training process, the location information is also included, which is the longitude and latitude of the observation. Some decision trees pick up these features. These trees divide the global extent into several zones. The observation location belongs to zones divided by different trees. Thus, we obtain a bag of boundaries. The maximums of the boundaries in each direction are regarded as the dividing lines. Every observation is surrounded by a rectangle of dividing lines, and others within one observation’s zones are considered neighbors. The neighboring zones differ by location. Every respondent has her or his neighbor zone; thus, we obtain 89,273 neighbor zones, which are geographically local. The local relationship is estimated based on one observation and others located in its neighboring zone; thus, the relationship coefficients also spatially vary. The estimation process is as follows:

where \({\alpha }_{jx}\) and \({\beta }_{jx}\) are the slope and the intercept of the local relationship between feature \(j\)’s value and its SHAP value based on \(x\)’s neighbor zone, \({X}_{x}^{j}\) is a vector of the feature \(j\)’s values in \(x\)’s neighbor zone, and \({S}_{jx}\) is a vector of the SHAP values corresponding to \({X}_{x}^{j}\). According to the local relationship coefficient, we could interpret the marginal contribution of an increase in a certain feature to mental health. To improve the geographical continuity of the relationship and emphasize the difference between each point in the same neighboring zone, we add geographical weights to the coefficient estimation process. We calculate the local geographical weight vector as geographically weighted regression methods^23,54 as follows:

where \({{\varvec{W}}}_{x}\) is the geographical weight vector of the elements in \(x\)’s neighbor zone, \({{\varvec{d}}}_{x}\) is a vector of distances between \(x\) and the elements in \(x\)’s neighbor zone, and \({h}_{x}\) is the farthest distance of the distance vector \({{\varvec{d}}}_{x}\). According to this equation, the weights of the elements with the furthest distance in \(x\)’s neighbor zone are always zero, while the aim observation \(x\) always has the largest weight, 1, in the regression. With the geographical weight vector, the local coefficient is estimated as follows:

where \({Coef}_{jx}\) is the estimated local coefficient, including \({\alpha }_{jx}\) and \({\beta }_{jx}\). Because we have 89,273 geographically local datasets, we eventually obtain 89,273 sets of local coefficients, which spatially vary.

Monetary values of land cover

To make the impacts of land cover change on mental health understandable and comparable, we estimate the monetary values of land cover. This method is friendly to the public because it is free of considerable background knowledge. We take the marginal substitution rate (MSR) of land cover and income as the monetary values, and it is estimated as follows:

where \({MSR}_{jx}\) is the MSR of feature \(j\) in observation \(x\)’s location, and \({\alpha }_{INCx}\) is the local relationship coefficient between the income value and its SHAP value based on the observations in \(x\)’s neighbor zone. In this equation, we require either the coefficients \({\alpha }_{jx}\) and \({\alpha }_{INCx}\) to be significant (p value < 0.1), or the MSR to be set to zero.

where \({MV}_{jx}\) is the monetary value of feature \(j\) in observation \(x\)’s location, and \({GDPPC}_{x}\) is the GDP per capita of respondent \(x\)’s country in the surveyed year. Based on these equations, the monetary values can be explained by how much income changes equal a 1% increase in a specific land cover.

Analysis roadmap

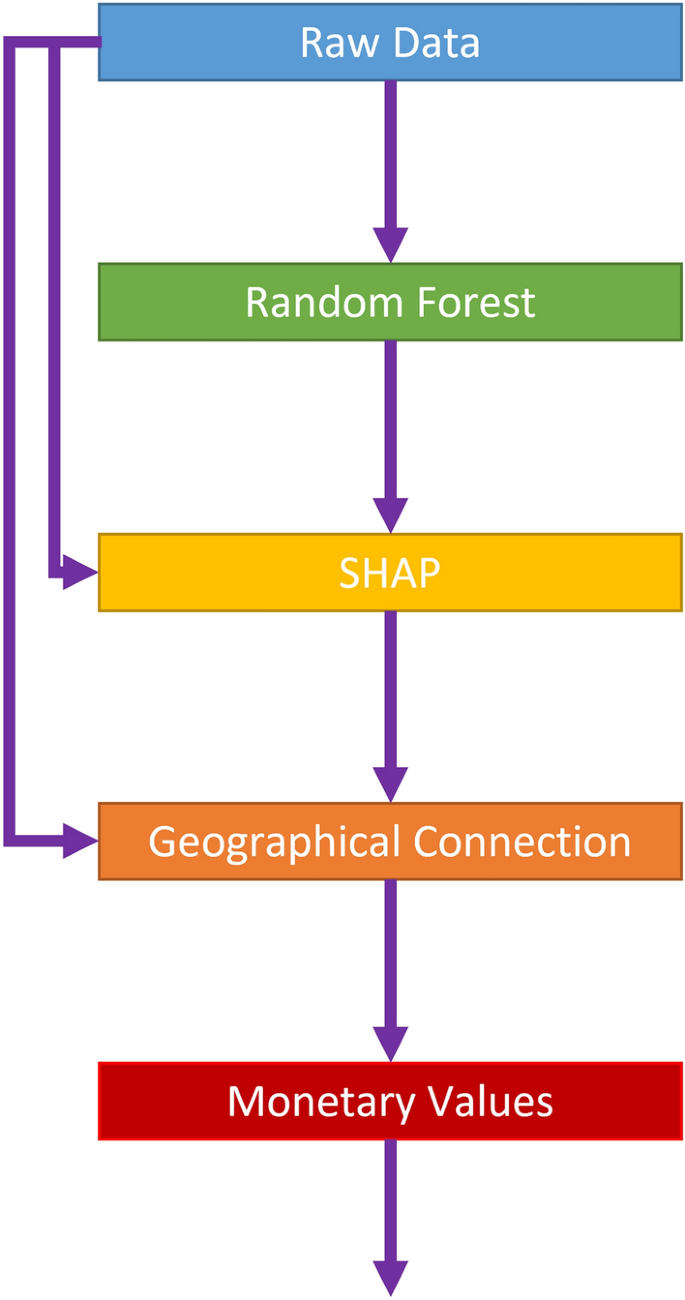
Figure 2 demonstrates our analysis roadmap from raw data to monetary values. First, we use the raw data to train a high-accuracy random forest. The random forest model is nonparametric, which means that the contribution of each variable is not straightforward. In this way, we take the second step to estimate the contribution of each variable value to mental health by using SHAP values. Importantly, SHAP values depict the contribution of current values of variables to mental health individually. A positive SHAP value indicates that the current variable values positively contribute to mental health, and vice versa. In other words, in the current study, we regard SHAP values as highlighting people’s attitude toward their current status. However, we do not know how variations in the current values affect SHAP values. Hence, we should use some method to connect the SHAP values with real values. Since this study covers the whole world, a statistic global analysis might lead to a biased relationship. Therefore, in the third step, we employ geographically weighted regression and local datasets to investigate the local coefficients individually. In fact, for each respondent, the coefficients of relationships between values of the variables of interest and their contribution to mental health can be spatially varied. For an individual respondent, a positive coefficient for a variable indicates that as the variable increases, its contribution to mental health also increases. Simply, the local coefficients of geographical connection represent the people’s attitude toward variations in variables of interest, and they are not directly related to the current values. In the fourth step, we use the local coefficients of each respondent to calculate monetary values. These monetary values can also differ among the respondents. They are not directly affected by the current variable values. These monetary values help make people’s attitudes toward the variation in variables easily understandable.